张量

张量是N维矩阵:

标量是 0 维张量
Vector 是一维张量
矩阵是一个二维张量

张量是一个概括向量和矩阵到更高的维度。

标量

向量

矩阵

张量

1	2	3
4	5	6

1	2	3
4	5	6

4	5	6
1	2	3

张量秩

张量可以具有的方向数氮维空间，称为秩张量的。

等级表示为右。

标量是一个数字。

它有 0 个轴
它有一个排名 0
它是一个 0 维张量

向量是一个数字数组。

它有 1 个轴
它有一个排名1
它是一个一维张量

矩阵是一个二维数组。

它有 2 轴
它有一个排名2
它是一个二维张量

实张量

从技术上讲，以上都是张量，但是当我们谈论张量时，我们通常谈论维度大于 2 的矩阵（R > 2）。

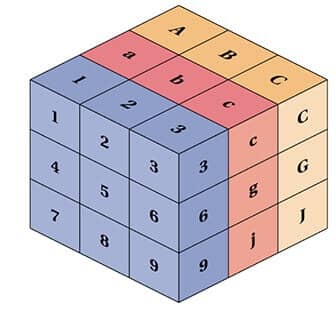
JavaScript 中的线性代数

在线性代数中，最简单的数学对象是标量:

const scalar = 1;

另一个简单的数学对象是数组:

const array = [ 1, 2, 3 ];

矩阵是二维数组:

const matrix = [ [1,2],[3,4],[5,6] ];

向量可以写为矩阵只有一列：

const vector = [ [1],[2],[3] ];

向量也可以写成数组:

const vector = [ 1, 2, 3 ];

张量是N 维数组:

const tensor = [ [1,2,3],[4,5,6],[7,8,9] ];

JavaScript 张量运算

在 JavaScript 中对张量运算进行编程很容易变成循环的意大利面条。

使用 JavaScript 库将为您省去很多麻烦。

用于张量运算的最常见的库之一称为张量流.js。

张量加法

const tensorA = tf.tensor([[1, 2], [3, 4], [5, 6]]);
const tensorB = tf.tensor([[1,-1], [2,-2], [3,-3]]);

// Tensor Addition
const tensorAdd = tensorA.add(tensorB);

// Result [ [2, 1], [5, 2], [8, 3] ]

亲自试一试 »

张量减法

const tensorA = tf.tensor([[1, 2], [3, 4], [5, 6]]);
const tensorB = tf.tensor([[1,-1], [2,-2], [3,-3]]);

// Tensor Subtraction
const tensorSub = tensorA.sub(tensorB);

// Result [ [0, 3], [1, 6], [2, 9] ]

亲自试一试 »

了解有关张量流的更多信息...