码农教程 - 一技在手,衣食无忧! tools

线性回归

❮ 上一节 下一节 ❯

回归是一种确定一个变量之间关系的方法（y）和其他变量（X）。

在统计学中，一个线性回归是一种对 y 和 x 之间的线性关系进行建模的方法。

在机器学习中，线性回归是一种监督机器学习算法。

散点图

这是散点图（来自上一章）：

示例

const xArray = [50,60,70,80,90,100,110,120,130,140,150];
const yArray = [7,8,8,9,9,9,10,11,14,14,15];

// Define Data
const data = [{
  x:xArray,
  y:yArray,
  mode: "markers"
}];

// Define Layout
const layout = {
  xaxis: {range: [40, 160], title: "Square Meters"},
  yaxis: {range: [5, 16], title: "Price in Millions"},
  title: "House Prices vs. Size"
};

Plotly.newPlot("myPlot", data, layout);
亲自试一试 »

预测值

从上面零散的数据，我们如何预测未来的价格呢？

  • 使用手绘线性图
  • 建立线性关系模型
  • 建立线性回归模型

线性图

这是一个根据最低和最高价格预测价格的线性图：

示例

const xArray = [50,60,70,80,90,100,110,120,130,140,150];
const yArray = [7,8,8,9,9,9,9,10,11,14,14,15];

const data = [
  {x:xArray, y:yArray, mode:"markers"},
  {x:[50,150], y:[7,15], mode:"line"}
];

const layout = {
  xaxis: {range: [40, 160], title: "Square Meters"},
  yaxis: {range: [5, 16], title: "Price in Millions"},
  title: "House Prices vs. Size"
};

Plotly.newPlot("myPlot", data, layout);
亲自试一试 »

来自上一章

线性图可以写成y = ax + b

在哪里：

  • y是我们想要预测的价格
  • A是线的斜率
  • X是输入值
  • 乙是截距

线性关系

这个模型使用价格和尺寸之间的线性关系预测价格：

示例

const xArray = [50,60,70,80,90,100,110,120,130,140,150];
const yArray = [7,8,8,9,9,9,10,11,14,14,15];

// Calculate Slope
let xSum = xArray.reduce(function(a, b){return a + b;}, 0);
let ySum = yArray.reduce(function(a, b){return a + b;}, 0);
let slope = ySum / xSum;

// Generate values
const xValues = [];
const yValues = [];
for (let x = 50; x <= 150; x += 1) {
  xValues.push(x);
  yValues.push(x * slope);
}
亲自试一试 »

在上面的示例中，斜率是计算出的平均值，截距 = 0。

使用线性回归函数

这个模型使用线性回归函数预测价格：

示例

const xArray = [50,60,70,80,90,100,110,120,130,140,150];
const yArray = [7,8,8,9,9,9,10,11,14,14,15];

// Calculate Sums
let xSum=0, ySum=0 , xxSum=0, xySum=0;
let count = xArray.length;
for (let i = 0, len = count; i < count; i++) {
  xSum += xArray[i];
  ySum += yArray[i];
  xxSum += xArray[i] * xArray[i];
  xySum += xArray[i] * yArray[i];
}

// Calculate slope and intercept
let slope = (count * xySum - xSum * ySum) / (count * xxSum - xSum * xSum);
let intercept = (ySum / count) - (slope * xSum) / count;

// Generate values
const xValues = [];
const yValues = [];
for (let x = 50; x <= 150; x += 1) {
  xValues.push(x);
  yValues.push(x * slope + intercept);
}
亲自试一试 »

多项式回归

如果分散的数据点不适合线性回归（通过点的直线），则数据可能适合多项式回归。

多项式回归与线性回归一样，使用变量 x 和 y 之间的关系来找到通过数据点绘制直线的最佳方法。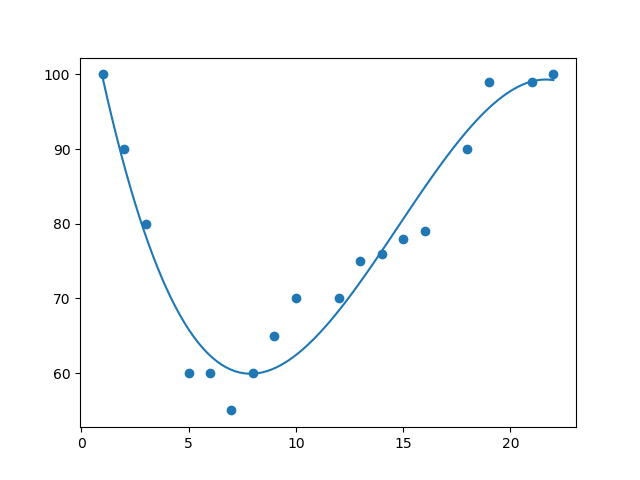Polynormal Regression

❮ 上一节 下一节 ❯