机器学习

学习是循环的

机器学习模型是训练有素经过循环播放多次传输数据。

对于每次迭代，重量值进行了调整。

当迭代失败时训练完成降低成本。

训练我找到最适合的线：

亲自试一试 »

梯度下降

梯度下降是解决人工智能问题的流行算法。

一个简单的线性回归模型可用于演示梯度下降。

线性回归的目标是将线性图拟合到一组 (x,y) 点。这可以用数学公式来解决。但一个机器学习算法也可以解决这个问题。

这就是上面的例子所做的。

它从散点图和线性模型 (y = wx + b) 开始。

然后它训练模型找到一条适合绘图的线。这是通过改变线的权重（斜率）和偏差（截距）来完成的。

下面是一个代码训练对象可以解决这个问题（以及许多其他问题）。

训练对象

创建一个 Trainer 对象，该对象可以在两个数组 (xArr,yArr) 中获取任意数量的 (x,y) 值。

将权重设置为零，将偏差设置为 1。

必须设置学习常数（learnc），并且必须定义成本变量：

示例

function Trainer(xArray, yArray) {
  this.xArr = xArray;
  this.yArr = yArray;
  this.points = this.xArr.length;
  this.learnc = 0.00001;
  this.weight = 0;
  this.bias = 1;
  this.cost;

成本函数

解决回归问题的标准方法是使用 "Cost Function" 来衡量解决方案的好坏。

该函数使用模型中的权重和偏差 (y = wx + b)，并根据线条与图的拟合程度返回错误。

计算此误差的方法是循环遍历图中的所有 (x,y) 点，并对每个点的 y 值与直线之间的平方距离求和。

最传统的方法是对距离进行平方（以确保为正值）并使误差函数可微。

this.costError = function() {
  total = 0;
  for (let i = 0; i < this.points; i++) {
    total += (this.yArr[i] - (this.weight * this.xArr[i] + this.bias)) **2;
  }
  return total / this.points;
}

的另一个名字成本函数是误差函数。

该函数中使用的公式实际上是这样的：

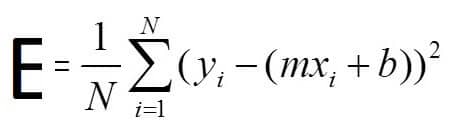
乙是误差（成本）
氮是观察总数（点）
y是每个观察值（标签）
X是每个观察值（特征）
米是斜率（权重）
乙是截距（偏差）
MX+B是预测
1/N * NΣ1是平方平均值

火车功能

我们现在将运行梯度下降。

梯度下降算法应该使成本函数走向最佳线。

每次迭代都应将 m 和 b 更新为成本较低（错误）的线。

为此，我们添加一个训练函数，多次循环所有数据：

this.train = function(iter) {
  for (let i = 0; i < iter; i++) {
    this.updateWeights();
  }
  this.cost = this.costError();
}

更新权重函数

上面的训练函数应该在每次迭代中更新权重和偏差。

移动方向使用两个偏导数计算：

this.updateWeights = function() {
  let wx;
  let w_deriv = 0;
  let b_deriv = 0;
  for (let i = 0; i < this.points; i++) {
    wx = this.yArr[i] - (this.weight * this.xArr[i] + this.bias);
    w_deriv += -2 * wx * this.xArr[i];
    b_deriv += -2 * wx;
  }
  this.weight -= (w_deriv / this.points) * this.learnc;
  this.bias -= (b_deriv / this.points) * this.learnc;
}

创建您自己的图书馆

图书馆代码

现在您可以在 HTML 中包含该库：

亲自试一试 »