机器学习 - 训练/测试

评估你的模型

在机器学习中，我们创建模型来预测某些事件的结果，就像在上一章中，当我们知道汽车的重量和发动机尺寸时，我们预测了汽车的二氧化碳排放量。

为了衡量模型是否足够好，我们可以使用称为训练/测试的方法。

什么是训练/测试

训练/测试是一种衡量模型准确性的方法。

之所以称为训练/测试，是因为您将数据集分为两组：训练集和测试集。

80%用于训练，20%用于测试。

你火车使用训练集的模型。

你测试使用测试集的模型。

火车该模型意味着创造该模型。

测试模型均值检验模型的准确性。

从数据集开始

从您想要测试的数据集开始。

我们的数据集展示了商店中的 100 位顾客以及他们的购物习惯。

示例

import numpy
import matplotlib.pyplot as plt
numpy.random.seed(2)

x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x

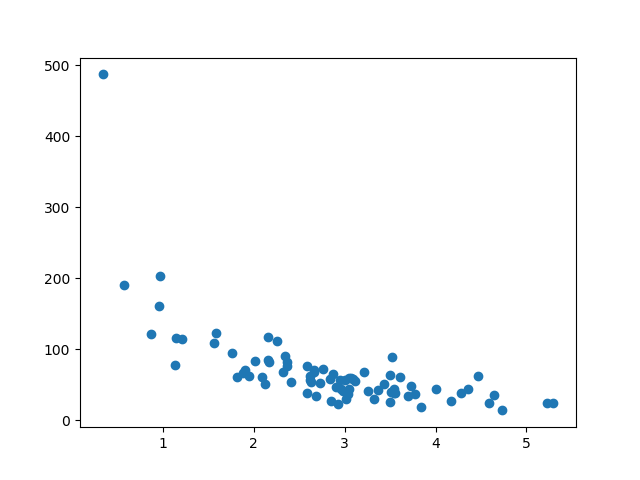
plt.scatter(x, y)
plt.show()

结果：

x 轴表示购买前的分钟数。

y 轴代表购买所花费的金额。

运行示例 »

分为训练/测试

这个训练集合应该是随机选择的80%的原始数据。

这个测试设置应该是剩下的20%。

train_x = x[:80] train_y = y[:80] test_x = x[80:] test_y = y[80:]

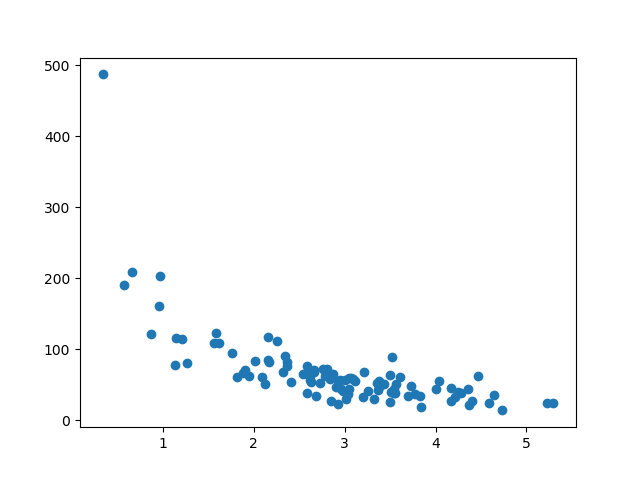
显示训练集

显示与训练集相同的散点图：

示例

plt.scatter(train_x, train_y)
plt.show()

结果：

它看起来像原始数据集，所以它似乎是一个公平的选择：

运行示例 »

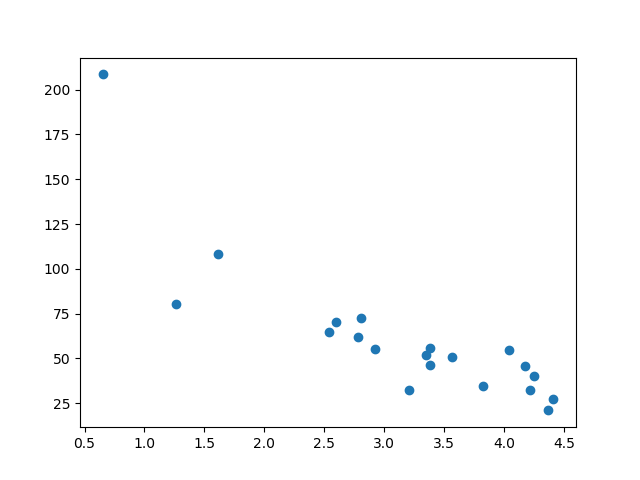
显示测试集

为了确保测试集不是完全不同，我们还将查看测试集。

示例

plt.scatter(test_x, test_y)
plt.show()

结果：

测试集也看起来像原始数据集：

运行示例 »

拟合数据集

数据集是什么样的？在我看来，我认为最合适的是多项式回归，所以让我们画一条多项式回归线。

要通过数据点绘制一条线，我们使用 plot()matplotlib模块的方法：

示例

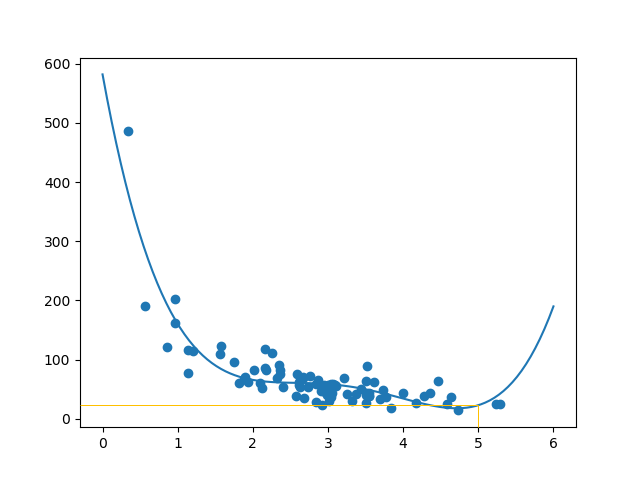
通过数据点绘制多项式回归线：

import numpy
import matplotlib.pyplot as plt
numpy.random.seed(2)

x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x

train_x = x[:80]
train_y = y[:80]

test_x = x[80:]
test_y = y[80:]

mymodel = numpy.poly1d(numpy.polyfit(train_x, train_y, 4))

myline = numpy.linspace(0, 6, 100)

plt.scatter(train_x, train_y)
plt.plot(myline, mymodel(myline))
plt.show()

结果：

运行示例 »

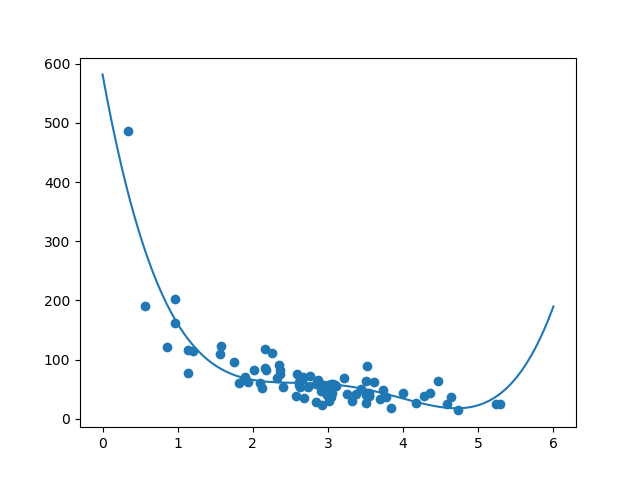
结果可以支持我对数据集拟合多项式回归的建议，尽管如果我们尝试预测数据集之外的值，它会给我们一些奇怪的结果。示例：该行表明顾客在商店里呆了 6 分钟将购买值 200 美元的商品。这可能是过度拟合的迹象。

但是 R 平方分数呢？ R 平方分数可以很好地指示我的数据集与模型的拟合程度。

R2

还记得 R2，也称为 R 平方吗？

它衡量x轴和y轴之间的关系，取值范围为0到1，其中0表示没有关系，1表示完全相关。

sklearn 模块有一个方法叫做r2_score()这将帮助我们找到这种关系。

在这种情况下，我们想要衡量顾客在商店停留的时间与他们花费的金额之间的关系。

示例

我的训练数据在多项式回归中的拟合效果如何？

import numpy
from sklearn.metrics import r2_score
numpy.random.seed(2)

x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x

train_x = x[:80]
train_y = y[:80]

test_x = x[80:]
test_y = y[80:]

mymodel = numpy.poly1d(numpy.polyfit(train_x, train_y, 4))

r2 = r2_score(train_y, mymodel(train_x))

print(r2)

亲自试一试 »

笔记：结果 0.799 表明存在良好关系。

引入测试集

现在我们已经建立了一个还可以的模型，至少在训练数据方面是这样。

现在我们也想用测试数据来测试模型，看看是否给出了相同的结果。

示例

让我们找到使用测试数据时的 R2 分数：

亲自试一试 »

笔记：结果 0.809 表明该模型也适合测试集，我们有信心可以使用该模型来预测未来值。

预测值

现在我们已经确定我们的模型没问题，我们可以开始预测新值。

示例

如果购买顾客在商店停留 5 分钟，她会花多少钱？

print(mymodel(5))

运行示例 »

该示例预测客户将花费 22.88 美元，如下图所示：