数据科学 - 斜率和截距
斜率和截距
现在我们将解释如何找到函数的斜率和截距:
f(x) = 2x + 80
下图指向斜率 - 表示直线的陡峭程度,以及截距 - 表示当 x = 0(对角线与垂直轴相交的点)时 y 的值。红线是上一页蓝线的延续。
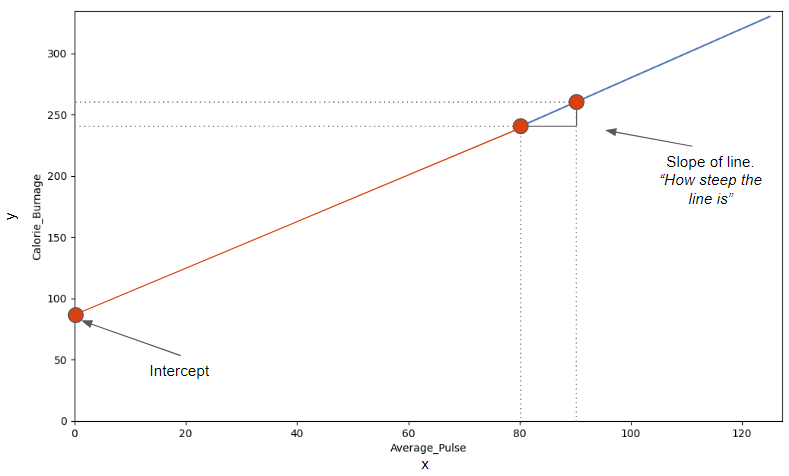
找到斜坡
斜率定义为平均脉搏增加 1 时卡路里燃烧量增加的量。它告诉我们"steep" 对角线是怎样的。
我们可以通过使用图中两点的比例差来找到斜率。
- 如果平均脉搏为 80,则卡路里燃烧量为 240
- 如果平均脉搏为 90,则卡路里燃烧量为 260
我们看到,如果平均脉搏增加 10,卡路里燃烧量就会增加 20。
Slope = 20/10 = 2
坡度为2。
在数学上,斜率定义为:
Slope = f(x2) - f(x1) / x2-x1
f(x2) = 第二次观测 Calorie_Burnage = 260
f(x1) = 第一次观察到的 Calorie_Burnage = 240
x2 = Average_Pulse 的第二次观察 = 90
x1 = Average_Pulse 的第一次观察 = 80
Slope = (260-240) / (90 - 80) = 2
保持一致,以正确的顺序定义观察结果!如果不是的话,预测就不会正确!
使用 Python 求坡度
使用以下代码计算斜率:
找到截距
截距用于微调函数预测 Calorie_Burnage 的能力。
如果完全绘制的话,截距是对角线与 y 轴相交的位置。
截距是 x = 0 时 y 的值。
在这里,我们看到,如果平均脉搏 (x) 为零,则卡路里燃烧量 (y) 为 80。
因此,截距为 80。
有时,截距具有实际意义。有时不是。
平均脉搏为零有意义吗?
不,你会死,而且你肯定不会燃烧任何卡路里。
然而,我们需要包含截距,以便完成数学函数正确预测 Calorie_Burnage 的能力。
数学函数的截距具有实际意义的其他示例:
- 使用营销支出预测明年的收入(如果营销支出为零,明年我们将有多少收入?)。人们可能会认为,即使公司不花钱进行营销,它仍然会有一些收入。
- 燃料使用量与速度(如果速度等于 0 英里/小时,我们使用多少燃料?)。使用汽油的汽车在闲置时仍会使用燃油。
使用 Python 求斜率和截距
这个np.polyfit()函数返回斜率和截距。
如果我们继续执行以下代码,我们可以从函数中获取斜率和截距。
示例
import pandas as pd
import numpy as np
health_data = pd.read_csv("data.csv", header=0, sep=",")
x = health_data["Average_Pulse"]
y = health_data["Calorie_Burnage"]
slope_intercept = np.polyfit(x,y,1)
print(slope_intercept)
亲自试一试 »
示例解释:
- 将变量 Average_Pulse (x) 和 Calorie_Burnage (y) 从 health_data 中分离出来。
- 调用 np.polyfit() 函数。
- 函数的最后一个参数指定函数的阶数,在本例中为"1"。
提示:线性函数 = 1. 度函数。在我们的示例中,该函数是线性的,在 1 度范围内。这意味着所有系数(数字)都是一的幂。
现在我们已经计算了斜率 (2) 和截距 (80)。我们可以将数学函数写成如下:
使用数学表达式预测 Calorie_Burnage:
f(x) = 2x + 80
任务:
现在,如果平均脉搏为 135,我们想要预测卡路里燃烧量。
请记住,截距是一个常数。常数是不改变的数字。
我们现在可以用 135 替换输入 x:
f(135) = 2 * 135 + 80 = 350
如果平均脉搏为 135,则卡路里燃烧量为 350。
在 Python 中定义数学函数
这是完全相同的数学函数,但是是用 Python 编写的。该函数返回 2*x + 80,其中 x 作为输入:
尝试将 x 替换为 140 和 150。
用 Python 绘制新图
在这里,我们绘制了与之前相同的图表,但稍微格式化了轴。
y 轴的最大值现在为 400,x 轴的最大值为 150:
示例
import matplotlib.pyplot as plt
health_data.plot(x ='Average_Pulse', y='Calorie_Burnage', kind='line'),
plt.ylim(ymin=0, ymax=400)
plt.xlim(xmin=0, xmax=150)
plt.show()
亲自试一试 »
示例解释
- 导入matplotlib库的pyplot模块
- 根据 Average_Pulse 和 Calorie_Burnage 绘制数据
kind='line'告诉我们我们想要哪种类型的情节。在这里,我们想要一条直线- plt.ylim() 和 plt.xlim() 告诉我们希望轴开始和停止的值。
- plt.show() 向我们显示输出