数据科学 - 线性回归

我们缺少一个影响 Calorie_Burnage 的重要变量，即训练的持续时间。

持续时间与 Average_Pulse 结合将更准确地解释 Calorie_Burnage。

线性回归

当您尝试查找变量之间的关系时，会使用术语回归。

在机器学习和统计建模中，这种关系用于预测事件的结果。

在本模块中，我们将讨论以下问题：

我们是否可以得出结论：Average_Pulse 和 Duration 与 Calorie_Burnage 相关？
我们可以使用 Average_Pulse 和 Duration 来预测 Calorie_Burnage 吗？

最小二乘法

线性回归使用最小二乘法。

这个概念是通过所有绘制的数据点画一条线。该线的定位方式应尽量缩短与所有数据点的距离。

该距离称为"residuals" 或"errors"。

红色虚线表示从数据点到绘制的数学函数的距离。

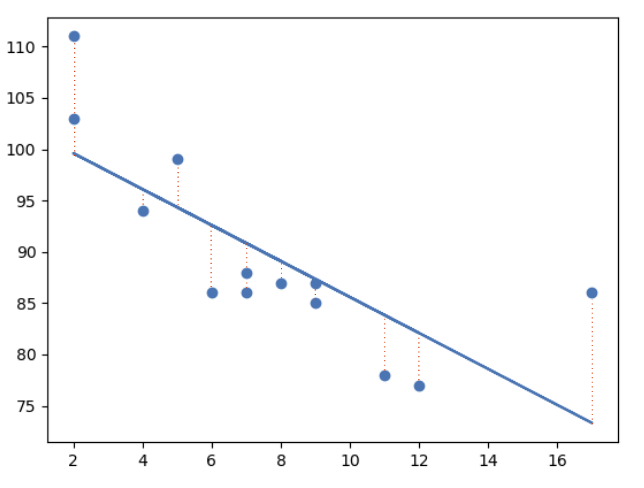
使用一个解释变量的线性回归

在此示例中，我们将尝试使用线性回归通过 Average_Pulse 来预测 Calorie_Burnage：

示例

import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats

full_health_data = pd.read_csv("data.csv", header=0, sep=",")

x = full_health_data["Average_Pulse"]
y = full_health_data ["Calorie_Burnage"]

slope, intercept, r, p, std_err = stats.linregress(x, y)

def myfunc(x):
return slope * x + intercept

mymodel = list(map(myfunc, x))

plt.scatter(x, y)
plt.plot(x, slope * x + intercept)
plt.ylim(ymin=0, ymax=2000)
plt.xlim(xmin=0, xmax=200)
plt.xlabel("Average_Pulse")
plt.ylabel ("Calorie_Burnage")
plt.show()

亲自试一试 »

示例解释：

导入您需要的模块：Pandas、matplotlib 和 Scipy
将 Average_Pulse 隔离为 x。将 Calorie_burnage 隔离为 y
通过以下方式获取重要的关键值：斜率、截距、r、p、std_err = stats.linregress(x, y)
创建一个使用斜率和截距值返回新值的函数。这个新值表示相应 x 值在 y 轴上的放置位置
通过该函数运行 x 数组的每个值。这将产生一个新数组，其中 y 轴有新值： mymodel = list(map(myfunc, x))
绘制原始散点图：plt.scatter(x, y)
绘制线性回归线： plt.plot(x, mymodel)
定义轴的最大值和最小值
标记轴："Average_Pulse" 和 "Calorie_Burnage"

输出：

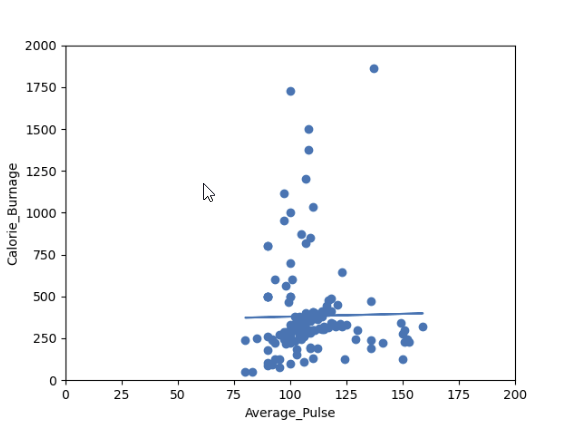
Linear Regression - One variable - Least Square

您认为这条线能够准确预测 Calorie_Burnage 吗？

我们将证明，仅变量 Average_Pulse 不足以对 Calorie_Burnage 进行精确预测。