数据科学 - 线性函数

作为数据科学家，了解数学函数很重要，因为我们想要做出预测并解释它们。

线性函数

在数学中，函数用于将一个变量与另一个变量相关联。

假设我们考虑卡路里燃烧和平均脉搏之间的关系。可以合理地假设，一般来说，卡路里燃烧量会随着平均脉搏的变化而变化——我们说卡路里燃烧量取决于平均脉搏。

此外，可以合理地假设，随着平均脉搏的增加，卡路里燃烧也会增加。卡路里燃烧和平均脉搏是要考虑的两个变量。

因为卡路里燃烧取决于平均脉搏，所以我们说卡路里燃烧是因变量，平均脉搏是自变量。

因变量和自变量之间的关系通常可以使用公式（函数）进行数学表达。

线性函数具有一个自变量 (x) 和一个因变量 (y)，并具有以下形式：

当我们选择自变量的值时，此函数用于计算因变量的值。

解释：

• f(x) = 输出（因变量）
• x = 输入（自变量）
• a = 斜率 = 是自变量的系数。它给出因变量的变化率
• b = 截距 = 是 x = 0 时因变量的值。它也是对角线与垂直轴相交的点。

具有一个解释变量的线性函数

具有一个解释变量的函数意味着我们使用一个变量进行预测。

假设我们想使用平均脉搏来预测卡路里燃烧量。我们有以下公式：

这里，数字和变量的含义是：

• f(x) = 输出。这个数字是我们获得 Calorie_Burnage 预测值的地方
• x = 输入，即 Average_Pulse
• 2 = 斜率 = 指定当 Average_Pulse 增加 1 时 Calorie_Burnage 增加多少。它告诉我们"steep" 对角线是怎样的
• 80 = 截距 = 固定值。它是 x = 0 时因变量的值

绘制线性函数

术语线性意味着"straight line"。因此，如果以图形方式显示线性函数，则该线将始终是直线。该线可以向上、向下倾斜，并且在某些情况下可以是水平或垂直的。

以下是上述数学函数的图形表示：

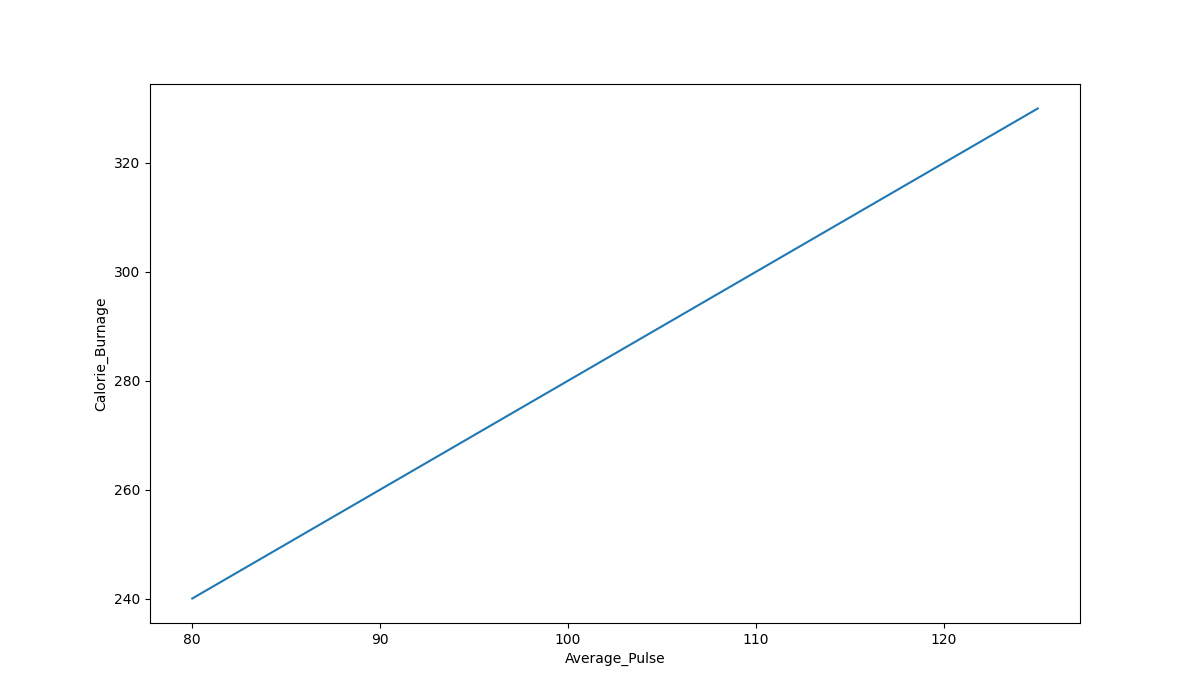
图表说明：

• 水平轴通常称为x轴。这里，它代表Average_Pulse。
• 垂直轴通常称为y轴。在这里，它代表 Calorie_Burnage。
• Calorie_Burnage 是 Average_Pulse 的函数，因为假定 Calorie_Burnage 取决于 Average_Pulse。
• 换句话说，我们使用 Average_Pulse 来预测 Calorie_Burnage。
• 蓝色（对角线）线代表预测卡路里消耗的数学函数的结构。